

Quantum gates for cat-state qubits
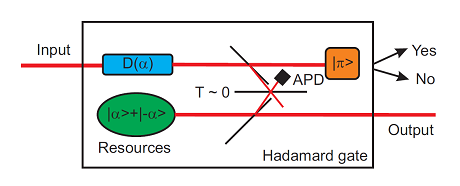
Figure 1: Schematic of the Hadamard gate. In the experimental realization, the resource state was replaced by a squeezed state and the |p> projector was a homodyne detector; if the quadrature measurement outcome fall within a certain interval and the APD is firing, the output is projected onto a Hadamard transformed state.
A schematic of the Hadamard gate is presented in Fig. 1. The scheme based on a squeezed state resource, linear operations and two projective measurements; a discrete variable and a continuous variable measurement. The input state - a coherent state superposition - is first displaced by an amount equal to the excitation of the coherent states of the computational basis. A single photon is then jointly subtracted from the displaced input state and a resource state (a coherent state superposition state) by means of beam splitters and a single photon counter. Finally, the state is projected onto an amplitude quadrature using a homodyne detector, and the remaining mode falls into the Hadamard transformed state. By injecting the computational basis states (|a> and |-a>) into the gate the function of the gate was characterized by reconstructing the Wigner functions of the transformed output states and calculating the fidelity with ideally transformed state.
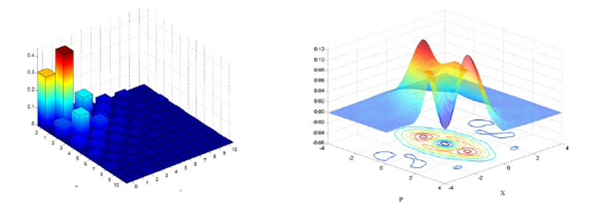
Figure 2: Density matrix and Wigner function for the output state for |a> as the input state. The Fidelity to the ideal output state is F=94%.
The gate was implemented using a squeezed state as a resource in replacement of the coherent state superposition state as the overlap between these two states was more than 90%. The squeezed state is produced through down-conversion in a periodically poled KTP crystal pumped with pico-second pulses at 415nm, thus producing pulsed squeezed light at 830nm. As an input state either |a> or |-a> was used which are displaced to |0> and |2a>. To further simplifyy the scheme, the input state is defined in the same spatial mode as the ancillae squeezed state but in orthogonal polarization modes; this facilitate the mixing of the two modes in a waveplate followed by a polarizing beam splitter. By jointly subtracting a single photon from the two states using an APD and by conditioning the output on successful measurement outcomes, the final state is formed and fully characterized by means of homodyne tomography.
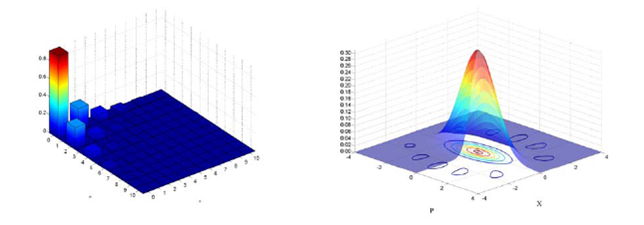
Figure 3: Density matrix and Wigner function for the output state for |-a> as the input state. The fidelity to the ideal output state is F=51%.
The results of a Hadamard transform of the two inputs, |a> and |-a>, are shown in Fig. 2 and 3. We present the density matrices and the Wigner functions of the two outputs, and compute the fidelities to the ideally transformed states.
The sign-flip operation transforms an odd photon-number Schrödinger cat to an even one, and conversely. This gate was experimentally implemented by an application of the photon subtraction operator, which can be approximated by a sampling beamsplitter of low reflectivity followed by a detection event on a photon counter. There have been demonstrations of such an effect, but so far the characterization has focused on the states that could be produced by this technique, rather than on the device itself.
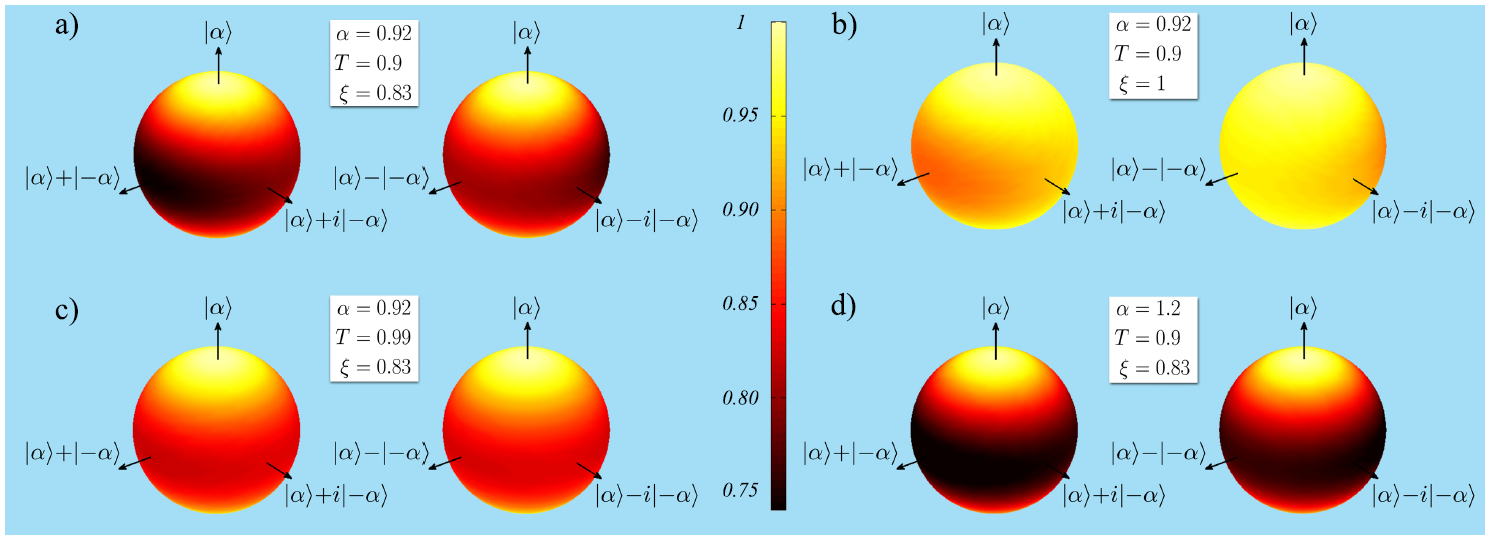
Figure 4: Fidelities of the output states for arbitrary ideal inputs represented on the Bloch sphere a) for our phase gate; b) for a perfect modal purity equal to 1; c) for a device with T = 0:99; d) for our device with a=1.2.
Due to decoherence processes, gates in a coherent states architecture most likely will not leave the output state inside the original reduced Hilbert space spanned by coherent states qubits. Moreover, the current technologies do not even warrant that input test states belong to this space. Therefore, one cannot simply use standard techniques, such as process tomography, for a characterization. In the present experiment these gates were characterize following a procedure which does not rely on a black-box approach, but requires some modelling of the functioning of the gate. One can identify a small number of parameters, accessible to the experimentalist, by which the gate process can be modelled (in the present case we have: the amplitude a of the coherent states, the transmission T of the sampling beamsplitter, and the modal purity). The behaviour of the device can then be obtained for ideal inputs, see Fig. 4.
Nondeterministic optical noiseless amplifier
The operating principle is depicted on the figure below: a single photon is split on an asymmetric beamsplitter (A-BS) with reflectivity r; a small amplitude coherent state |α> is superimposed with the reflected output of the A-BS on a symmetric beamsplitter (S-BS). A successful run of the amplifier is flagged by a single photon event on detector D1 and no photons on detector D2. Conditioned on this event, the transmitted output of the A-BS is the amplified coherent state |gα>, where the value of g depends on the chosen reflectivity r of the A-BS.
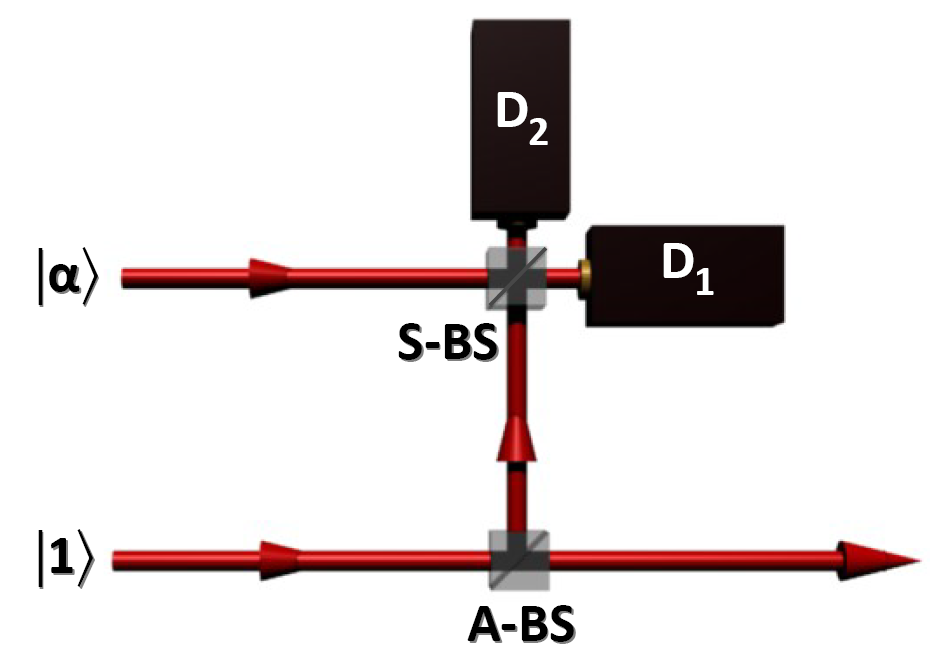
Figure 1: Conceptual layout of the noiseless amplifier.
The effective amplification was quantified by introducing an effective gain geff of the amplifier. Experimental data compared well with a model taking into account the main imperfections of the setup: limited quality of our single photon state, due to multipair emission and parasitic processes, imperfect mode-matching between the single photon and the coherent beams, or finite photon counting detection efficiency. The noiseless behavior of our amplifier is analyzed in terms of its “equivalent input noise" Neq, which tells how much noise must be added to the input noise level, in order to mimic the observed output noise for a given gain: Negative values for this quantity were clearly observed, shows that our device not only amplifies the signal but also increases the signal-to-noise ratio. Obviously it remains compatible with Quantum Laws because this phenomenon is observed only for specific heralded events whose outcome rate is as low as the gain is high.
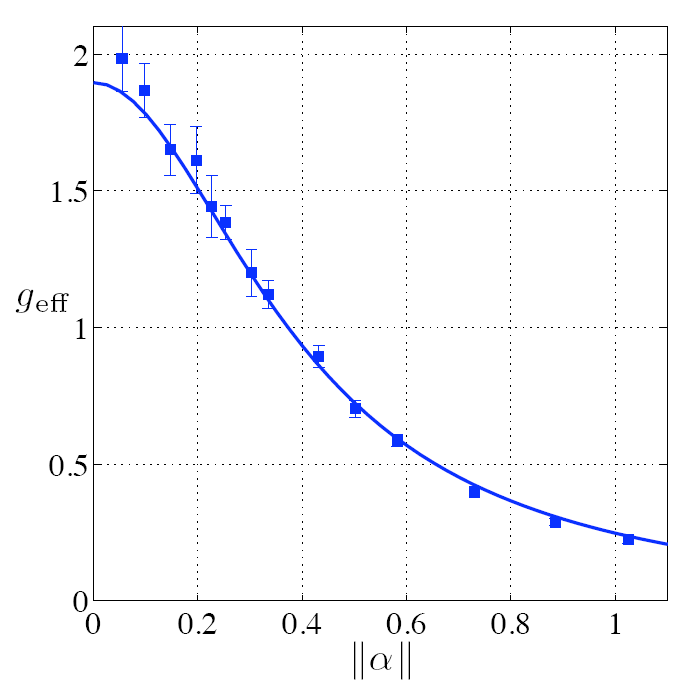
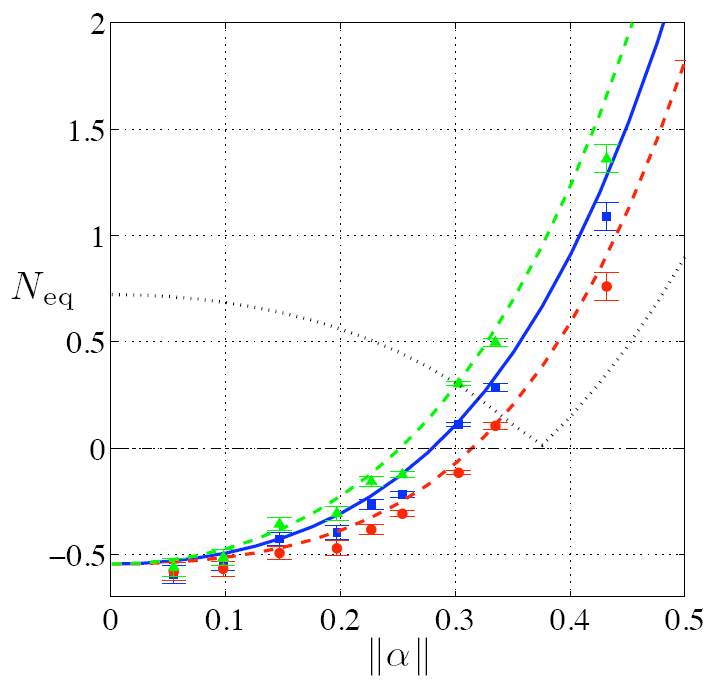
Figure 2: (Left) Experimental results for the effective phase-independent gain (markers) compared with model (lines) as a function of the input state amplitude. (Right) Experimental results for the Equivalent Input Noise: Average value (squares), maximal value (triangles), and minimal value (circles), compared with model (lines).
The performance of conditional noiseless amplification can be significantly improved by replacing the quantum scissors by a sequence of single-photon addition and single-photon addition. This scheme which is illustrated in Fig. 3 has been experimentally tested by Partner UP in collaboration with the group of Professor Marco Bellini at INOA, Florence.
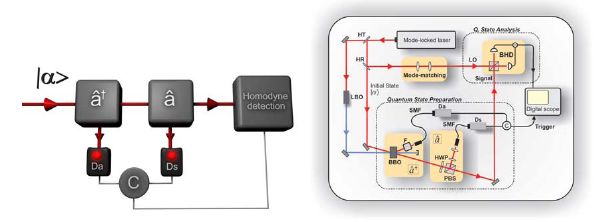
Figure 3: Conceptual scheme (left) and detailed experimental setup (right) of hifi noiseless amplifier. Da and Ds denote single photon detectors, HT (HR) is a high transmissivity (reflectivity) beam splitter; LBO is a lithium triborate crystal for frequency doubling; SMF are single mode fibers; F is a narrow spectral filter.
In the experiment, two blocks for conditional single-photon addition and subtraction are placed in the path of a coherent state. A coincident click (C) from the two on/off photo-detectors Da and Ds heralds the successful realization of the probabilistic noiseless amplification of the input coherent state. High-frequency, time-domain, balanced homodyne detection is then used for a full reconstruction of the involved quantum states. The amplifier was thoroughly characterized for a range of input coherent states with amplitude up to =1. In particular, the effective gain of the amplifier, quadrature variances, and fidelity of the amplified state were determined. The experimental results confirm that this high-fidelity noiseless amplifier with nominal gain g=2 achieves the best level of effective gain and final state fidelity ever reached and adds only very little noise.
Remarkably, the challenging operation of single photon addition can be replaced by addition of thermal noise while still retaining some crucial properties of the noiseless amplifier. In particular, the resulting scheme is capable of probabilistically increasing the phase information of coherent states based on the addition of thermal noise prior to a weak photon number resolving measurement.
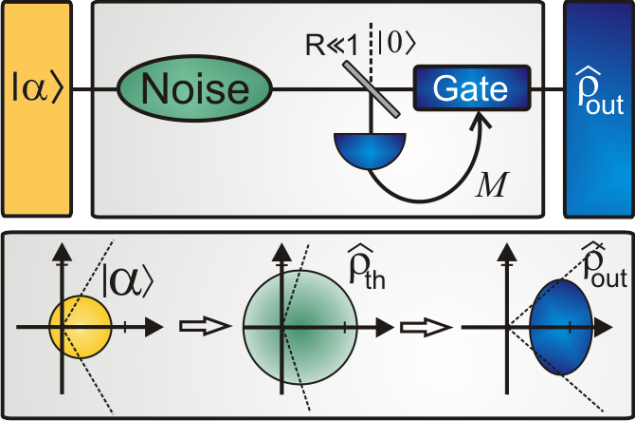
Figure 4: (top) Sketch of the scheme. First, the input coherent state is mixed with thermal noise. A small portion of the state is measured and the remaining part is heralded according to the outcome of the measurement. (bottom) Evolution of the coherent state during the phase concentration cycle. The heralding on high number of detections leads to an effectively amplified state with decreased phase variance, as indicated by the dashed lines.
A sketch of the scheme is shown in Fig. 4. A coherent state with unknown phase entering the setup is mixed with thermal noise. It is subsequently split asymmetrically into two parts. The weaker part is sent to a photon number resolving detector PNRD, where it provides the information used to herald the output state. The brighter part is sent to a gate, that can be passed, when the number of clicks in the detector equals or surpasses a given threshold value M. The heralding procedure thereby exploits the classical correlations between the transmitted and tapped-off part of the beam, that have been introduced by the addition of thermal noise. A high number of detections in the tap beam is correlated to a high amplitude in the transmitted beam
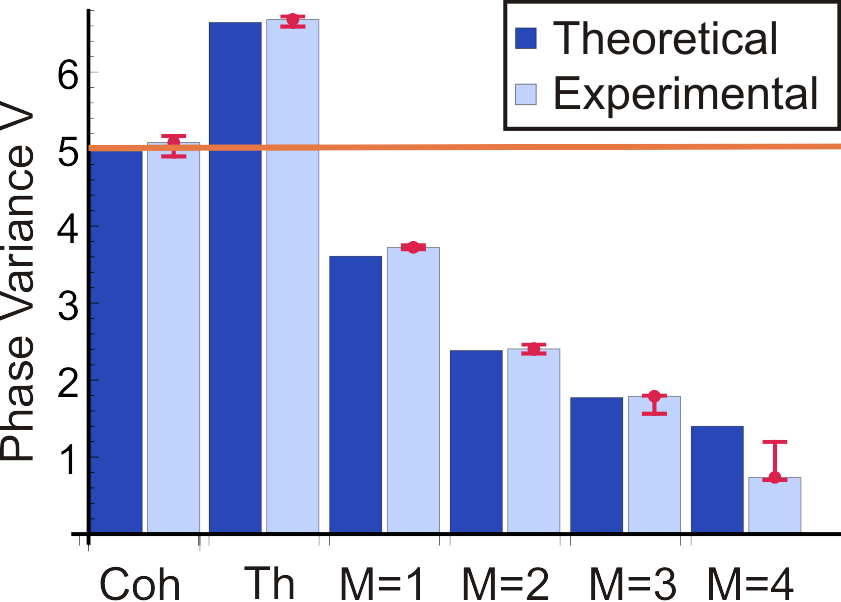
Figure 5: Experimental and theoretical results for the phase variance of the input coherent state (Coh), the input state after the mixing with thermal noise (Th) and the heralded output states (M=1, …, M=4). Enhanced phase information is already observed for a heralding threshold of just a single click in the detector.
We verified the increase of phase information in an experimental implementation by homodyne tomography of the heralded states for threshold values of up to four clicks in the detector. We derived the Holevo phase variance as a measure for the phase uncertainty and compared the results for various threshold parameters with our theoretical model. We could clearly observe the enhanced phase information, yet for a threshold of only a single click in the detector, as presented in Fig. 5.
Publications:
F. Ferreyrol, M. Barbieri, R. Blandino, S. Fossier, R. Tualle-Brouri, and P. Grangier, Implementation of a nondeterministic optical noiseless amplifier, Phys. Rev. Lett. 104, 123603 (2010).
A. Zavatta, J. Fiurášek, and M. Bellini, A high-fidelity noiseless amplifier for quantum light states, Nature Photonics 5, 52–56 (2011).
M. A. Usuga, C. R. Müller, C. Wittmann, P. Marek, R. Filip, Ch. Marquardt, G. Leuchs and U. L. Andersen, Noise-powered probabilistic concentration of phase information, Nature Physics 6, 767–771 (2010)
Experimental demonstration of CV quantum error correction protecting against erasures
Quantum information processing
relies on the
robust and faithful transmission, storage and manipulation of quantum
information. However, since errors are inherent to any realistic
implementation, the future of quantum information systems strongly
relies on
the ability to detect and correct for these errors.
We have proposed and
experimentally implemented
a scheme for combating erasure errors in a continuous variable (CV)
quantum
channel. More specifically, we have devised a CV quantum
erasure-correcting
code, which protects coherent states of light against complete erasure.
As
shown in figure 1, the scheme encodes two coherent states into a
bi-partite
entangled state, thus resulting in a four-mode erasure code. The two
ancillary
squeezed vacuum states are produced in two optical parametric
oscillators and
the coherent state is generated at a 5.5MHz sideband employing
amplitude and
phase modulators. Subsequently, the four-mode code is launched into
four
free-space channels that independently and randomly erase the conveyed
beams.
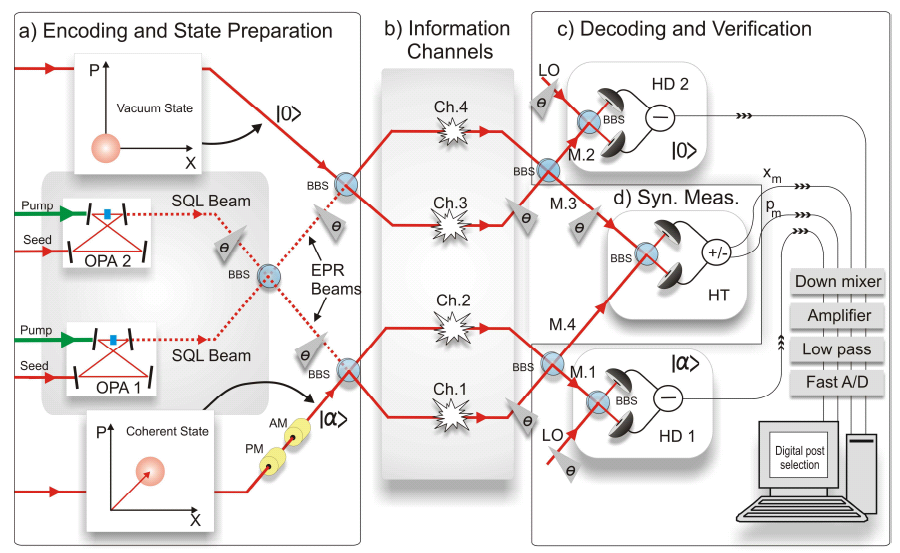
Fig. 1: Schematic
setup of the quantum erasure correcting code.
After transmission, the
receiving beams are
brought to interference as shown in the figure and the error is
subsequently
probed in a syndrome measurement where conjugate quadratures are
detected.
Errors in the remaining beams are then corrected based on the outcome
of the
syndrome measurements. We have been investigating two different kinds
of error
correction: Deterministic correction where all states are actively
displaced as
a function of the syndrome outcomes, and a probabilistic correction
where noise
affected states are filtered out if an error was detected in the
syndrome
measurement. The former approach only allows for a single error (at the
time)
and the location of the error must be a priori know, whereas the latter
approach allows for multiple erasures and ignorance about the location
of the
erasures.
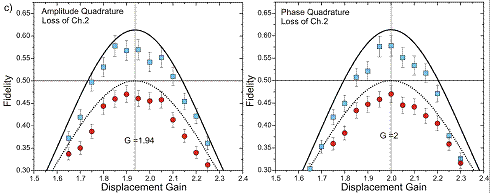
Fig. 2: Protocol
fidelity as a
function of the displacement gain for deterministic quantum erasure
correcting
coding.
The protocol is quantified in
terms of the
transmission fidelity and the results for the deterministic and
probabilistic
protocols are shown in figures 2 and 3, respectively. In figure 2, the
fidelity
is plotted as a function of the displacement gain both for the
entanglement
based error code (blue squares) and without entanglement. We find
maximum
fidelities of 58% which clearly surpasses the classical benchmark of
50%.
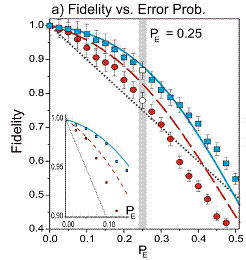
Fig. 3: Protocol
fidelity as a
function of the error probability for probabilistic recovery of quantum
information.
Publications:
J. Niset, U.L. Andersen and
N.J. Cerf, Experimentally Feasible Quantum
Erasure
Correcting Code for Continuous Variables, Phys. Rev. Lett. 101, 130503 (2008).
>> First version of the CV QIP roadmap prepared by the COMPAS consortium is available on-line.
>> Project COMPAS officially started on 1st of April, 2008
for Research of the European Commission, under the FET-Open grant agreement COMPAS, number 212008.